INGRESADO. FELICES FIESTAS

El día 11 de diciembre, me tuve que ir a urgencias aquejado de fuertes dolores abdominales. Quedé ingresado, se me diagnosticó pancreatitis. Hoy 26, quince días después y debido a las fechas en las que estamos, se me ha permitido regresar a casa, eso si, con una dieta muy severa. Ese es el motivo de no haber publicado nada en todo este tiempo.

OS DESEO PASÉIS UNAS FELICES FIESTAS Y QUE EL 2009 OS COLME DE TODO LO QUE VUESTRAS ALMAS NECESITAN.

LA CÁLIDA ALFOMBRA Y EL FRÍO MÁRMOL

Si estamos en el invierno, cuando escribo este artículo, en Granada hace mucho frío, habremos experimentado, la agradable sensación de pisar descalzos una buena alfombra de lana. Que distinta sensación tenemos al pisar un suelo de mármol, aunque dicho suelo, por estar al lado de la alfombra, esté a la misma temperatura.
¿Qué motivo hay para que estando alfombra y mármol a la misma temperatura, la sensación al pisarlos, sea tan distinta?
El motivo no es otro que su distinta conductividad térmica.

Además, de la transmisión de energía, en forma en este caso de calor, del cuerpo que más energía tiene, al que tiene menos.
La conductividad térmica es una propiedad física de los materiales que mide la capacidad de conducción de calor. Es elevada en metales y en general en cuerpos continuos, y es baja en los gases, siendo muy baja en algunos materiales especiales como la fibra de vidrio, que se denominan por eso aislantes térmicos.

Para que exista conducción térmica hace falta una sustancia, de ahí que es nula en el vacío ideal, y muy baja en ambientes donde se ha practicado un vacío elevado. Es el caso de los termos, que logran mantener por mucho tiempo, los líquidos a la temperatura a la que los hemos guardado.
La alfombra está construida con lana, un mal conductor térmico y como resultante un buen aislante, pero además, atrapa entre sus fibra aire, otro mal conductor térmico y buen aislante.
Lo contrario le pasa al mármol, que es un buen conductor y mal aislante.
Por ello, al pisar el mármol, como nuestro cuerpo está a más temperatura que él y siendo éste un buen conductor, al intentar igualarse las temperaturas, “roba” rápidamente el calor de nuestro pie, lo que nos hace sentir esa sensación de frío ( desagradable si es invierno, agradable si es en verano )

EL EFECTO BOTIJO

Todos hemos bebido agua fresca de un botijo. Alguna vez nos hemos podido preguntar, el motivo de que el botijo mantenga el agua a una temperatura considerablemente inferior a la del ambiente.
El botijo está hecho de una materia porosa, los botijos pintados y de superficies brillantes, pueden ser muy bonitos, pero no mantienen el agua igual de fresca. Esa materia porosa hace que el agua de su interior empape la superficie, rezume. Ese agua que impregna la superficie, se evapora. Para evaporarse, necesita energía y esa energía la toma del agua interior del recipiente, logrando de esta simple manera bajar la temperatura.
La energía que "roba" el agua al evaporarse es aproximadamente 600 calorías por gramo de agua evaporada.
Evidentemente el que el botijo "haga" un agua más o menos fresca, depende mucho de las condiciones exteriores. Por ejemplo, si el botijo está en un lugar aireado y seco, enfriará más que en un lugar húmedo. Por eso un botijo, enfriará más en la montaña que en la playa.
En condiciones óptimas estos recipientes, pueden llegar a bajar la temperatura del agua de su interior, entre unos 10 y 15 º C. que no está nada mal.
El efecto es el mismo que se produce cuando sudamos, el sudor tiene como misión el bajar la temperatura del cuerpo. Al evaporarse el sudor, necesita energía, al tomar esta energía, hace que la temperatura de la piel y por lo tanto del cuerpo, baje.
Cuando nos ponemos un pañuelo mojado en el cuello, pasa lo mismo.
Cuando a un enfermo, se le ponen toallitas mojadas en la frente o en otras partes del cuerpo, se busca lo mismo, la bajada de la temperatura por el proceso de evaporación del agua.
En los pueblos, es muy normal ver en los días de verano, a las mujeres con un cubo en una mano y esparciendo ( rociando ) agua en la puerta de la casa con la otra. Tengo en mis recuerdos esa imagen ya al atardecer, momentos antes de sacar las sillas, para sentarse en agradables tertulias estivales.
Estamos, otra vez, procurando bajar la temperatura por el mismo efecto, la energía que necesita el agua para evaporarse, sólo que en este caso, en vez de tomarla del agua, la toma del medio ambiente, haciéndolo así algo más fresco y soportable

LOS IONES NEGATIVOS SON LOS POSITIVOS

Muchas veces, cuando estamos en ciertos ambientes, experimentamos una gran sensación de bienestar.

Seguro que hemos podido observar que esa sensación, siempre se da en unas circunstancias concretas. La mayoría de las veces, tiene su explicación científica.

Empecemos por definir que son los iones.

Se define al ion o ión, del griego (ἰών, "el que va"), como una especie química, ya sea un átomo o una molécula cargada eléctricamente. Esto se debe a que ha ganado o perdido electrones de su dotación, originalmente neutra, fenómeno que se conoce como ionización.
Los iones cargados negativamente, producidos por la ganancia de electrones, se conocen como aniones (que son atraídos por el ánodo) y los cargados positivamente, consecuencia de una pérdida de electrones, se conocen como cationes (los que son atraídos por el cátodo).

El ser humano, se encuentra mucho mejor en un ambiente cargado negativamente, es decir con iones negativos, que en un ambiente cargado con iones positivos, de ahí el título de este artículo.

LOS INONES NEGATIVOS SON LOS POSITIVOS para la salud, claro está.

Vamos a centrarnos, en una tarde de cielo gris plomizo, con densas nubes que amenazan tormenta.

¿ Cómo nos encontramos ante esa situación? Normalmente, nos encontramos pesados, densos, incluso con cierta tendencia hacia estados depresivos o al menos de abatimiento..

Por fin, se desarrolla una fuerte tormenta, rayos, lluvia, etc.. Al final cesa.. Salimos a dar un paseo, ¿ Cómo nos encontramos ahora ? Estamos mucho más relajados, las tensiones han cesado, como también, el mal estado incluso de pesimismo que antes nos embargaba.

¿ Qué ha pasado ? Antes de las tormentas, la atmósfera está cargada con iones positivos. Cuando estalla la tormenta, los rayos, la lluvia, el arrastrar el agua las particulas de polvo de la atmósfera, etc. Todos esos efectos combinados, hacen que la atmósfera se cargue de iones negativos, ese es el verdadero motivo de que antes de la tormenta, nos encontremos densos, pesados, mal en general y después, nos encontremos mucho mejor.

La naturaleza, las plantas, las cascadas de agua, las fuentes, liberan iones negativos. No es por lo tanto casualidad que nos encontremos tan bien, a la orilla de los cursos de agua y más si se producen cascadas.

El polvo, los humos, los productos sintéticos, atrapan los iones negativos y hacen que la atmósfera quede cargada de forma positiva y por eso son malos para nuestra salud.

¿ Os habéis parado a pensar, el motivo de que sea tan gratificante un paseo por EL GENERALIFE?

Hay plantas que son más eficaces, a la hora de cargar el ambiente de forma negativa ( recordemos, positiva para la salud ). Es el caso de todas las familias de los cactus.

Actualmente muchos modelos de aire acondicionado, son a la vez ionizadores, es decir, cargan el ambiente de iones negativos.
El artículo de hoy, es un motivo más para que tratemos con cariño a esos seres vivos que tenemos dentro de nuestras casas. Me refiero a las plantas. Además de ayudarnos de otra muchas formas, también nos crean un ambiente más saludable para vivir.
( Tened en cuenta que las plantas por la noche "respiran" y consumen también oxígeno, al contrario que hacen durante el día, que como consecuencia de la función clorofílica, lo liberan. No se deben tener por ese motivo, demasiadas plantas en el recinto donde dormimos)

ANTENAS PARABÓLICAS

Las antenas para recibir señales de diversos tipos, son parabólicas.

Alguna vez nos podemos haber preguntado, el motivo de tener ese tipo de simetría y no otro. Por ejemplo ¿por qué las antenas no son una semi esfera?

La sección de una antena parabólica es evidéntemente, una parábola. La parábola es la cónica que resulta, al cortar una superficie cónica, por un plano paralelo a la generatriz del cono.

La parábola es el lugar geométrico de puntos del plano , tales que equidistan de un punto fijo llamado foco y de una recta denominada directriz.

La parábola tiene una propiedad muy importante.
Si trazamos la tangente a la parábola en un punto, esta 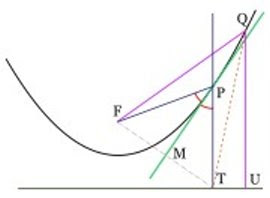tangente es bisectriz del ángulo que forman:

La recta obtenida al unir el foco con el punto de tangencia y la recta que pasando por dicho punto, es paralela al eje de simetría de la parábola.

La propiedad anterior tiene como consecuencia que la superficie parabólica, sea lo que se llama, una superficie reflectante, es decir, los rayos paralelos al eje de simetría de la parábola, son reflejados al incidir en la superficie parabólica, hacia el foco de la parábola.

Las aplicaciones prácticas son muchas.

Las antenas de satélites y radiotelescopios aprovechan la propiedad anterior para dirigir las señales recibidas desde un emisor lejano, hacia un receptor colocado en la posición del foco.

Si construimos un espejo de forma parabólica, los rayos del sol serán reflejados hacia el foco de la parábola, donde se podrá obtener una temperatura muy elevada.

En la Plataforma Solar de Tabernas ( Almería ) Podemos encontrar diversas aplicaciones de la propiedad anteriormente señalada. Algunas de ellas se muestran a continuación, en las fotografías que acompañan este artículo.




Arquímides, ya hizo uso de esta propiedad en el año 212 a.C. para prender fuego a los barcos enemigos desde lejos.

PROGRAMACIÓN LINEAL

PROBLEMA DE PROGRAMACIÓN LINEAL

Expongo aquí, resuelto, un problema típico de programación lineal.
Pretendo con ello, que mis alumnos de 1º de Bachillerato, vean una aplicación práctica de la resolución de los sistemas de inecuaciones con dos incógnitas, aunque la programación lineal no esté dentro del programa de la asignatura.
He decidido incluir este problema en mi blog, en vez de “subirlo” a mi wiki-espacio, por si una aplicación tan práctica de unas matemáticas elementales, pudieran ser de interés para algunas de las personas que visitan mi blog.
Como introducción diré que en 1939, el matemático ruso Leonidas V. Kantorovitch publica una extensa monografía, Métodos matemáticos de organización y planificación de la producción, en la que por primera vez, se tratan una gran gama de problemas con una teoría matemática muy concreta y precisa que hoy llamamos programación lineal.
En 1941-1942, se formula por primera vez el problema del transporte y lo hacen de forma independiente, por un lado Koopmans y por otro Kantorovitch.
Pero el desarrollo operativo de la programación lineal comienza en 1947, cuando George Bernard Dantzing hizo la primera formulación del METODO SIMPLEX.
Aquí, he usado para resolver el problema un método geométrico muy sencillo y lógico.
La programación lineal, se aplicó primeramente a problemas de nutrición ( problema de la dieta ) y después, a multitud de problemas de todo tipo, la mayor parte de las veces, estos problemas eran económicos.
En 1958, se aplican los métodos de la programación lineal, para calcular el plan óptimo de transporte de materiales, a las obras en Moscú.
Os dejo con un sencillo problema, con el que nos podemos hacer una idea de esta parte de las Matemáticas.

Una fábrica de bombones tiene almacenados 500 kg de chocolate, 100 kg de almendras y 85 kg de frutas. Produce dos tipos de cajas: la del tipo A contiene 3 kg de chocolate, 1 kg de almendras y 1 kg de frutas. Las del tipo B contienen 2 kg de chocolate, 1,5 de almendras y 1 de fruta. Los precios de las cajas de tipo A y B son respectivamente 7 € y 9 € ¿Cuantas cajas debe fabricar de cada tipo para maximizar su venta?

SOLUCIÓN
Lo primero que haremos, es ordenar los datos, nos facilitará el planteamiento de las inecuaciones que formarán la región factible.
La región factible es el recinto del plano que verifica todas las inecuaciones.
El número de cajas del tipo A que debemos fabricar le llamamos x.
El número de cajas del tipo B que debemos fabricar le llamamos y.
El chocolate total que emplearemos será 3x+2y , lógicamente, tendrá que ser menor ó igual que la cantidad de chocolate que tenemos…que son 500 kg.
Lo mismo con las almendras y la fruta.
Las inecuaciones que forman la región factible son:
3x+2y ≤ 500
x+1,5y ≤ 100
x + y ≤ 85
x ≥ 0
y ≥ 0

Las inecuaciones x ≥ 0 e y ≥ 0 son de pura lógica. Nunca podremos fabricar un número negativo de cajas Las dos inecuaciones antes citadas, definen el primer cuadrante del plano.
A continuación, dibujamos las rectas r-> 3x+2y = 500,

s->x +1,5 y = 100, t-> x+y = 85
r -> 3x+2y = 500, y = ( 500 - 3x) /2 Para x = 0 -> y = 250

Para x = 100 -> y = 100
s -> x +1,5 y = 100 por 2 -> 2x+3y = 200, y = ( 200 - 2x)/3

x = 100 -> y = 0 ; x=0 -> y =200/3 =Aprox 66,6
t -> x+y = 85, y = 85 – x Para x = 0 ->y = 85 Para x = 85->y = 0

La función que queremos hacer máxima, la venta total, será:

Z (x,y) = 7 x + 9 y

Dibujamos las rectas, a continuación, vemos qué semiplano en cada caso, verifica la inecuación correspondiente. Para ello y puesto que ninguna de las rectas pasa por el ( 0, 0 ) lo más fácil es dar este valor, viendo si verifica la inecuación o no. Si la verifica, será esa parte del plano la solución de la inecuación correspondiente, si no es así, será la otra parte del plano.

La región factible es el cuadrilátero OABC. En cualquiera de los puntos de ese recinto se verifican todas las inecuaciones.
Las coordenadas de A son ( 0 , 200/3). Para calcular las de B, hay q resolver el sistema dado por s y t ->B ( 55 , 30). Las coordenadas de C son (85,0)
Pero la función que queremos optimizar, en este caso maximizar, alcanzará su valor máximo en la frontera de dicho recinto, lo anterior es muy lógico pero su demostración, excede los objetivos que me he propuesto.

Vamos a evaluar la función Z, llamada función objetivo, en cada uno de los vértices del recinto.
Recordemos Z = 7 x + 9 y

En el O ( 0,0 ) evidéntemente Z = 0
ZA= 7 . 0 + 9 . 200/3 = 600 €
ZB = 7 . 55 + 9 . 30 = 655 €
ZC = 7 . 85 + 9 . 0 = 595 €

Maximiza por lo tanto B. Hay que fabricar 55 cajas del tipo A y 30 del tipo B para hacer la venta máxima.

Existe otra forma también muy usada, la de las rectas de nivel, pero creo que la anteriormente expuesta, se entiende muy bien.

ANALÓGICO Y DIGITAL

Puede parecer algo simple y sencillo, pero cuando a mis alumnos les pregunto por la diferencia entre analógico y digital, son minoría los que la conocen. Estoy hablando de alumnos de 4ºE.S.O. 1º y 2º de Bachillerato.
Leemos o escuchamos al cabo de la semana, muchísimas veces la palabra digital, pero ..¿Sabemos diferenciar analógico de digital?
Para comprender bien la diferencia, vamos a hablar antes de lo que es una variable continua y una variable discreta.
Para ello, lo mejor es que nos guiemos de unos ejemplos sencillos.
La altura de una persona, es una variable continua. Entre 170 cm y 174 cm, esa variable, puede tomar todos los valores intermedios, puede medir por ejemplo 172,5 cm. Es más, si una persona mide 173 cm., es seguro que en un momento de su vida ha medido 162,5 cm.
Una variable es continua, cuando puede tomar todos los valores dentro de un intervalo. Cuando nos referimos a todos los valores, nos estamos refiriendo a todos los nº reales que se pueden dar en ese intervalo.
Otro caso muy claro de variable continua, es el peso.
Entre 70 y 80 kg, una persona puede pesar todos los valores reales intermedios. Podemos perfectamente encontrar una persona que pese 72,250 Kg por ejemplo.
Hablemos ahora de otro tipo de variable, la variable discreta.
Para ello, nos vamos a fijar en el nº de alumnos de los distintos grupos de un curso, en un colegio. Puede ser que el grupo menos numeroso, tenga 20 alumnos y que el grupo más numeroso tenga 26 alumnos. Obviamente, no hay ningún grupo que pueda tener 23,5 alumnos.
Una variable es discreta, cuando no puede tomar todos los valores en un intervalo, en este caso el nº de alumnos es una variable discreta. Entre 20 y 26 alumnos, sólo se pueden dar, 20, 21, 22, 23, 24, 25 y 26 alumnos por grupo.
Otra variable discreta sería el nº de hijos de las familias de un bloque de piso.
Una vez entendido lo anterior, es muy fácil distinguir entre analógico y digital.
Trabajamos en forma analógica cuando podemos hacer una lectura de forma continua de la variable. Ejemplo. Un disco de vinilo ( los antiguos discos que veréis por casa ) almacena una señal de audio de forma continua. Así es, en el surco del disco se halla contenida TODA la información sobre la onda sonora.
Un CD almacena la señal de audio, de forma digital. Realmente lo que hay grabado en el CD es una lectura de la onda pero cada ciertos intervalos, aunque estos sean muy pequeños. Una vez hecha esa lectura, se codifica la señal en el sistema binario, a base de 0 y 1. Cuando escuchamos esa música, necesitamos un decodificador que haga el proceso inverso.
Las señales digitales, a diferencia de las señales analógicas, no varían de una forma continua, si no que lo hacen en pasos o incrementos discretos.
En un CD por bien que se escuche, no está grabada la onda sonora completa. Repito, lo que está grabado son lectura parciales de esa onda.
Lo que ocurre es que esas lecturas se hace cada tan poco tiempo, que sólo los oídos más entrenados y agudizados pueden distinguir la diferencia.
He conocido a personas, muy amantes de la música, que dicen distinguir perfectamente un sonido de un CD, de uno de un disco de vinilo.
No entro en las ventajas de cada uno de los sistemas, analógico y digital, sólo quiero exponer la diferencia fundamental entre ellos.
Resalto, como digo en el lateral de mi blog, que mi intención es motivar y animar a mis alumnos ( y todo aquel que entre ) divulgando aspectos matemáticos en particular y científicos en general, de una forma lo más clara y sencilla posible, no pretendo hacer un estudio exhaustivo de los temas tratados. Cada una de las personas que leen estas entradas, se interesarán por un tema u otro en concreto, en los que a través de los medios a su alcance, profundizarán como consideren oportuno.

El AZUL DEL CIELO

Alguna vez os habéis podido preguntar el motivo de que el cielo sea de color azul.
La luz que nos viene del Sol es poli-cromática, resultado de la suma de todos los colores que componen el arco iris.
Para llegar hasta nosotros, la luz que proviene de nuestra estrella, tiene que atravesar la atmósfera, en ella hay partículas y pequeñas gotitas de agua.
Sabemos que cuando la luz solar atraviesa un prisma, se produce el fenómeno de la refracción. La luz blanca se descompone en los distintos colores, debido a que cada longitud de onda (correspondientes a cada color ) tiene un distinto índice de refracción.
Se puede observar, que los colores violeta y azul son los más desviados, siendo el rojo el menos desviado.
Al atravesar la luz la atmósfera, las partículas que en ella hay, no tienen suficiente tamaño para detenerla, pero si para desviarla, produciéndose la dispersión. Las longitudes de onda corta, con mayor energía, son a las que les corresponde más dispersión, como estas longitudes corresponden a los colores violeta y azul, esos son los más desviados.
Ahora bien, el fenómeno de la dispersión, se produce una y otra vez, desviándose la luz en todas las direcciones, por eso a pesar de que la luz que nos llega, procede del Sol, nosotros, miremos en la dirección que miremos, vemos el cielo azul.
Cuando el Sol está bajo, cerca del horizonte, vemos que toma un color rojizo. Esto es debido a que cuando está en esa posición, los rayos tienen que atravesar mayor cantidad de atmosfera, eso provoca que de la luz blanca, los colores cercanos al azul en el arco iris, hayan sido dispersados en casi su totalidad, quedando sólo los tonos de mayor longitud de onda o menor energía, los correspondientes a las tonalidades del rojo.
Hemos visto que las partículas que hay en el aire, dispersan más el violeta y después el azul. Ahora bien, nosotros vemos el cielo azul, esto es debido a dos motivos principales.
Por un lado, la luz solar contiene más luz azul que violeta y por otro lado, el ojo humano es más sensible al azul que al violeta.

Si queremos profundizar más en el motivo de que el cielo sea azul, tendremos que explicar la llamada difusión de RAYLEIGH (en honor del físico inglés Lord Rayleigh que fue el primero en darle explicación)
Si las partículas que hay en la atmósfera, ya sean átomos aislados o pequeñas moléculas, son de un tamaño igual o inferior al de la longitud de onda de la luz incidente, la onda cede parte de su energía a la corteza atómica que comienza a oscilar, de manera que un primer efecto de la interacción de la luz con las partículas pequeñas del aire, es que la radiación incidente, cede parte de su energía y se debilita. Como es lógico, esta energía no se queda almacenada en el aire, pues cualquier átomo o partícula pequeña cuya corteza se agita, acaba radiando toda su energía en forma de onda electromagnética al entorno en cualquier dirección.
Rayleigh dedujo que la intensidad de la luz difundida es inversamente proporcional a la cuarta potencia de la longitud de onda. Se produce mayor dispersión, por lo tanto, para las ondas más cortas. La violeta y la azul son las más difundidas y el rojo con mayor longitud de onda, la que menos.
Si la luz solar se encontrara con partículas de mayor tamaño, la difusión Rayleigh, no se produciría y lo que ocurriría es la llamada difusión de Mie.
Si es la difusión de Mie la que se produce de forma masiva, la luz solar perdería su color blanco, tornándose más gris. Esto es lo que sucede en los días muy nublados, cuando las nubes son gruesas, el cielo se ve gris, a veces ese gris se hace casi negro.

LAS FRACTALES

Las fractales son objetos geométricos que tienen una propiedad, la AUTOSIMILITUD.
SU FORMA, SE MANTIENE CON INDEPENDENCIA DE LA ESCALA A LA QUE SE OBSERVE.
El nombre de fractal se lo dio B. Mandelbrot en 1975. En latín, fractus significa fracturado o quebrado.
Se definen estos objetos, mediante un algoritmo ( la mayor parte de las veces, muy simple ) recursivo o iterativo.

En la primera imagen, la fractal de Sierpinski, se ve muy bien como está construida.
La segunda imagen, nos muestra la fractal de Mandelbrot, posiblemente la más conocida.
La tercera y última imagen, es un caso muy claro de cómo las fractales, también se dan en la naturaleza. La fotografía corresponde a un tipo de brócoli, que en algunos lugares le llaman romanescu.

En mi Wiki-Espacio, en el apartado de "varios", he incluido un programa para dibujar fractales. Muy sencillo, práctico y útil. Tanto ese programa como el video cuyo enlace adjunto, se lo debemos a Alberto Rodríguez Santos, desde aquí mi más sincero agradecimiento.

Aconsejo ver este video, además de un claro ejemplo de la autosimilitud en las fractales, tiene una gran belleza.

Alta resolución

http://www.epsilones.com/imagenes/fractales/mandel-b.wmv

Si no puedes ver el video mediante el enlace anterior, prueba el siguiente, es con menos resolución pero tarda menos en cargarse.

http://www.epsilones.com/imagenes/fractales/mandel-m.wmv

EL TEOREMA DE PITÁGORAS

Pitágoras de Samos, nació en Jonia, en la isla de Samos hacia el 572 a de C.

Fue el fundador de la Escuela Pitagórica. Sus dos ideas fundamentales son:

- La transmigración de las almas.

Según esta teoría, las almas pasan de cuerpo en cuerpo, reencarnándose en sucesivas vidas.

- Los números son el principio de todas las cosas.

El famoso teorema que lleva su nombre es seguro que aunque se le atribuya a él, no fuera él quien lo descubriera. Dice, como bien sabéis, que en todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Geométricamente esto quiere decir, que si levantamos sobre la hipotenusa de un triángulo rectángulo, un cuadrado de lado esa hipotenusa, el área de ese cuadrado, es igual, a la suma de las áreas de los cuadrados levantados sobre cada cateto.

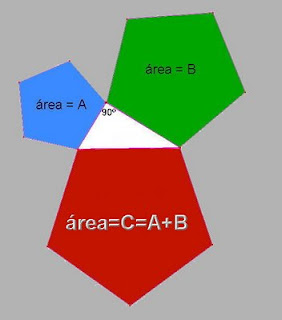
LO CURIOSO DE ESTE TEOREMA Y QUE NO ES TAN CONOCIDO, ES QUE ESE ENUNCIADO ES UNA PARTICULARIZACIÓN DE UN TEOREMA MÁS AMPLIO.
EN REALIDAD, SI CONSTRUIMOS CUALQUIER POLÍGONO REGULAR DE LADO LA LONGITUD DE LA HIPOTENUSA, EL ÁREA DE DICHO POLÍGONO, ES LA SUMA DE LAS ÁREAS DE LOS POLÍGONOS REGULARES ( DE IGUAL NÚMERO DE LADOS, OBVIAMENTE ) CONSTRUIDOS CON LADOS IGUALES A LA LONGITUD DE LOS CATETOS

DIOS NO JUEGA A LOS DADOS

¿ Has escuchado alguna vez esa frase ?

Esas palabras las dijo Albert Einstein ( Nobel de Física 1921 )

El Principio de Incertidumbre de Heisenberg ( Nobel de Física 1932 ), fundamental para la Mecánica Cuántica, dice que es imposible determinar simultáneamente, la posición de una partícula y su momento lineal o cantidad de movimiento ( m.v ). Quiere ésto decir, que si medimos con exactitud la velocidad de una partícula, no podremos determinar la posición en ese instante, nos deberemos conformar con calcular la probabilidad de que se encuentre en tal o cual posición. De ahí la frase de Einstein, " DIOS NO JUEGA A LOS DADOS"

A esta frase, Niels Bohr ( Nobel de Física 1922 ), con quien Einstein mantuvo una gran polémica por ese tema, muy famosa en el mundo de la ciencia, contestó, " Sr. Einstein, ¡ deje de decirle a Dios lo que debe hacer ! "

En las fotos. Albert Einstein y Niel Bohr

Aclaración. Un alumno me ha pedido que le explicara la relación entre lo anterior ( el Principio de Incertidumbre ) y la frase de Einstein, no lo veia claro.

Einstein no estaba de acuerdo con esa indeterminación en el Universo, de ahí las polémicas con Bohr, no estaba de acuerdo en que una vez determinada la velocidad, sólo se pudiera hablar de PROBABILIDAD y no certeza, en cuanto a la posición en ese instante de la partícula, de ahi la frase.

Los dados representan el azar, lo contrario a la determinación, a la certeza.

El efecto mariposa

Es muy probable que hayas oido hablar del "efecto mariposa" ¿Sabes a que se refiere dicho efecto?

En los sistemas caóticos, como el que rige el tiempo atmosférico, en el que intervienen muchas variables, una pequeña variación de las variables que forman las ecuaciones, tiene como consecuencia una gran variación en el resultado . Por eso se dice .. que el aleteo de una mariposa en Hong-Kong (es decir, una perturbación muy pequeña) puede hacer que esta tarde llueva en Londres.

¿ De dónde viene el nombre del famoso GOOGLE ?

Según parece el nombre de la famosa empresa Google principal adversario de Microsoft, viene de su similitud con Googol. Un Googol es un número tremendamente grande, 10 elevado a 100.

Un Googol es por lo tanto un 1 seguido de 100 ceros.

Para haceros una idea, todas las partículas que componen el universo conocido, no llegan a 10 elevado a 80.

La proporción Áurea Phi

- Nº de hembras / machos de una colmena = Phi

- Razón entre los diámetros de cada tramo en un Nautilos = Phi ( figura )

- Razón entre los diámetros de cada circulo en el girasol = Phi

- Altura de un hombre / distancia desde ombligo al suelo = Phi

- Distancia cadera suelo / distancia rodilla suelo = Phi

- Distancia hombro punta dedos / distancia codo dedos = Phi

- Dimensiones arquitectónicas del Partenón = Phi

- Pirámides de Egipto = Phi

- Sonatas de Mozart, La Quinta Sinfonía de Beethoven, trabajos de Debussy y Schubert

- Miguel Ángel, Durero, Leonardo da Vinci y muchos otros.

- Stradivarius lo empleaba para ubicar los oídos o efes.

- Pentagrama. En él sus líneas se cortan siguiendo la proporción áurea.

 

        

  (a+b) /a = a /b   Segmento total a+b es a a como a es a b = Phi

Rojo/Azul=Azul/Verde=/Verde/Morado = Phi

 Phi =  ( 1+raiz de 5) /2= 1´6180....

Phi = 1´61803....

 

Sucesión de Fibonacci 

  1,1,2,3,5,8,13,21, 34 

Según aumentan los términos de la  sucesión, si dividimos un término entre el inmediato anterior vamos obteniendo un número cada vez más aproximado a Phi.

 

Interesante video sobre Phi y

La sucesión de Fibonacci

 

http://es.youtube.com/watch?v=j9e0auhmxnc

Despues de ver ese video..

¿ No te infunden un tremendo respeto las Matemáticas?

¿ No te gustan un poco más..?

Pues eso es sólo una pequeña parte.....

 

MATRICES

DEFINICION.-Definimos matriz como un conjunto de números reales ordenados en filas y columnas.

a₁₁ a₁₂ a₁₃

a₂₁ a₂₁ a₂₂

Designaremos la matriz entre parentesis y sus elementos con una letra con dos subindices, el primero para las filas y el segundo para las columnas.

(a_ij) Matriz de i filas y j columnas.

a_ij Elemento que ocupa en la matriz la fila i y la columna j.

DIMENSION de una matriz es el pruducto indicado de filas por columnas. Ej.- Matriz de dimensión 2X3

Cuando tienen el mismo nº de filas que de columnas, llamaremos orden de la matriz al nº de filas ó columnas.

TIPOS DE MATRICES (1).

-Rectangulares.- M. que tienen distinto nº de filas que de columnas.

-Cuadradas.- M. con igual nº de filas que de columnas.

-M.Columna.- M. rectangular de dimensión nx1.

-M.Fila.- M. rectanngular de dimensión 1xm.

-M.Nula.- M. que tiene todos sus elementos nulos.

DIAGONAL DE UNA MATRIZ CUADRADA.-

-DIAGONAL PRINCIPAL es el conjunto de elementos a_ij / i=j

-DIAGONAL SECUNDARIA es el conjunto de elementos a_ij / i+j=n+1

n=orden de M.

TIPOS DE MATRICES (2)

-M. Diagonal.- Es una M. cuadrada que tiene nulos todos los elementos, excepto los de la diagonal principal.

Ej.

.

.

-M. Escalar.- Es la matriz diagonal cuyos elementos de la diagonal principal son todos iguales.

-M. Unidad.- Es la matriz escalar cuyos elementos distintos de 0 son iguales a 1.

-M. Triangular- Es la matriz cuadrada que tiene todos los elementos por encima o por debajo de la diagonal principal nulos.

Ej.

.

.

OPERACIONES CON MATRICES

IGUALDAD DE MATRICES.-Dadas dos M. de la misma dimensión, diremos que ambas son iguales cuando lo son sus elementos correspondientes.

(a_ij) = (b_ij) == i=j Vi,Vj

SUMA DE MATRICES.-En el cunjunto de las matrices rectangulares de dim. nxm , se define una ley de composición interna llamada suma de matrices como la siguiente aplicación:

M_nxm x M_nxm ----- M_nxm

((a_ij) , (b_ij))----- (a_ij)+(b_ij) = (a_ij+b_ij)

Es decir , a cada par de matrices rectangulares de dim. nxm, le hacemos corresponder otra matriz de la misma dim. cuyo elementos se obtienen sumando termino a termino los elementos correspondientes a cada matriz .

Ej.

.

.

.

PROPIEDADES de la suma de matrices.

-Conmutativa.-

(a_ij) + (b_ij) = (b_ij)+(a_ij)

-Asociativa.-

[(a_ij)+(b_ij)]+(c_ij)=(a_ij)+[(b_ij)+(c_ij)]

-Ele.Neutro.-

(a_ij)+(0)=(a_ij)

-Ele.Opuesto.-La M. opuesta de una dada es la que resulta de sustituir en la M. dada, cada elemento por su opuesto.

La M. opuesta actua como elemento opuesto en la suma de matrices. (a_ij)+(b_ij)=0

Todas estas propiedades son consecuencia de la definición de suma de matrices y de las correspondientes propiedades de los números reales. Como consecuencia de todas estas propiedades el conjunto de las matrices M_mxn respecto a la operación suma, tiene estructura de Grupo Abeliano.

PRODUCTO DE UN NUMERO REAL POR UNA MATRIZ.

En el conjunto M_mxn se define la ley de composición externa denominada producto de un número real por una matriz como la siguiente aplicación:

R x M_mxn -----------M_mxn

(t ,(a_ij)) -----------t.(a_ij)=(t.a_ij)

Es decir el producto de un número real por una matriz rectangular de dim. mxn, es otra matriz de la misma dim. cuyos elementos se obtienen multiplicando dicho número por todos los elementos de la matriz dada.

PROPIEDADES.

-Distributiva mixta del producto de un número real, respecto a la suma de matrices. t.[(a_ij)+(b_ij)]=t.(a_ij)+t.(b_ij)

-Distributiva mixta del producto de una matriz respecto a la suma de números reales. (a_ij).(t+p)=t.(a_ij)+p.(a_ij)

-Asociativa mixta. (t.p)[(a_ij)]=t.[p.(a_ij)]

-Elemento neutro para la ley externa. Elemento unidad.

1.(a_ij)=(a_ij).1=(a_ij)

EL ESPACIO VECTORIAL DE LAS MATRICES RECTANGULARES.

Por lo visto anteriormente, el cunjunto de las matrices rectangulares de dim. nxm respecto de la ley externa, producto de un número real por una matriz y respecto a la ley de composición interna, suma de matrices, tiene estructura de espacio vectorial sobre R.

( M_nxm,+,.R)-----Espacio vectorial.

PRODUCTO DE MATRICES.

En el conjunto M_nxm, en el conjunto M_mxp y en el conjunto M_nxp, se llama pruducto de matrices a la siguiente aplicación.

M_nxm x M_mxp ----------- M_nxp

((a_ij),(b_jk))------------- (a_ij).(b_jk)= a_ij.b_jk=c_ik

Es decir, los elementos de la matriz producto se obtienen sumando los productos que resultan de multiplicar, los elementos de la fila que ocupa el lugar i de la matriz (a_ij) por los elementos de la columna que ocupa el lugar k de la matriz (b_jk).

Observemos que para multiplicar matrices, el número de columnas del primer factor ha de ser igual al número de filas de la matriz que actua como segundo factor.

La dimensión de la matriz producto es nxp siendo:

n=Número de filas de la 1ª matriz

p=Número de columnas de la 2ª matriz

Ejemplos.:

.

.

.

.

.

Ejemplos.:

EN EL CONJUNTO DE LAS MATRICES CUADRADAS de orden n

se cumplen las siguientes propiedades del producto de matrices.

-Asociativa. [(a_ij).(b_jk)].(c_kr)=(a_ij).[(bjk).(c_kr)]

-Elem. neutro. La matriz unidad, actua como elem. neutro del

producto de matrices.

PROPIEDAD distributiva del producto respecto de la suma.

(a_ij).[(b_jk)+(c_jk)]=(a_ij).(b_jk)+(a_ij).(c_jk)

-IMPORTANTE.: El producto de matrices no es conmutativo.

EL ANILLO DE LAS MATRICES CUADRADAS.

Por todo lo dicho anteriormente podemos asegurar que el conjunto de las matrices de orden n con respecto a las dos leyes internas, suma y producto de matrices tiene estructura de anillo unitario no conmutativo.

( Mn,+,.)---Anillo unitario.

TRASPOSICION DE MATRICES.

Sean M_nxm y M_mxn, el conjunto de todas las matrices de dim. nxm y mxn respectivamente. Se llama trasposición de matrices a toda aplicación:

M_nxm-----------M_nxm

(a_ij)----------(a_ij)^t=(a_ji)

Es decir, dicha aplicación asocia a cada matriz de dim nxm, otra matriz de dim mxn, que se obtiene convirtiendo las filas en columnas sin alterar su orden.

Ejemplo.

.

.

.

.

.

TIPOS DE MATRICES.

-Matriz simétrica es aquella matriz que coincide con su traspuesta. Ej.:

.

.

.

-Matriz antisimétrica es aquella matriz que su opuesta coincide con su traspuesta. Ej.:

.

.

.

-Mariz ortogonal es aquella matriz cuadrada que cumple que el producto por su traspuesta es igual a la matriz unidad.

Ej.:

senx -cosx

cosx senx

DETERMINANTES

DEFINICIÓN DE DETERMINANTE

Sea M_n el conjunto de todas las matrices cuadradas de orden n y R el conjunto de los números reales. Se llama determinante de la matriz cuadrada a la aplicación que asocia a cada matriz A, el número real IAI que se llama determinante de A.

M_n---------R

A ---------IAI

El número real IAI se obtiene como la suma de todos los productos de n factores, cada uno de los cuales contiene un solo elemento de cada fila y un solo elemento de cada columna, anteponiéndole el signo + o - según las dos permutaciones formadas por los subíndices que indican las filas y las columnas de los n factores, sean de igual clase o distinta.

a₁₁ a₁₂ a₁₃

a₂₁ a₂₂ a₂₃ =

a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂-a₁₃a₂₂a₃₁-a₁₁a₂₃a₃₂-a₁₂a₂₁a₃₃

DETERMINANTE DE 2º Y 3º ORDEN. REGLA DE SARRUS

Para calcular un determinante de segundo orden, calculamos el producto de la diagonal principal y le restamos el producto de la diagonal secundaria.

DETERMINANTES DE TERCER ORDEN. REGLA DE SARRUS.

MENOR COMPLEMENTARIO Y ADJUNTO DE UN ELEMENTO.

Sea un determinante de orden n, y a_ij un elemento cualquiera. Se llama menor complementario de a_ij al determinante de orden n-1 que resulta de suprimir en el determinante dado la fila i-ésima y la columna j-ésima, es decir, la fila y la columna donde se encuentra el elemento.

El menor complementario de a_ij se representa _ij

Se llama adjunto del elemento a_ij al menor complementario de dicho elemento, anteponiendo el signo + o - según que la suma de los subíndices i+j sea par o impar.

El adjunto del elemento a_ij se designa por A_ij

A₂₃=

DESARROLLO DE UN DETERMINANTE POR LOS ADJUNTOS DE UNA LÍNEA.

Emplearemos el termino línea, para asignar indistintamente a una fila o a una columna.

El valor de un determinante es igual a la suma de los productos de los elementos de una línea por sus adjuntos correspondientes.

PROPIEDADES DE LOS DETERMINANTES.

1.: El valor de un determinante no varia si en él se cambian filas por columnas o viceversa, siempre que se mantenga el orden.

.

2.: Si en un determinante, se cambian entre si dos líneas paralelas, el valor absoluto de dicho determinante no cambia pero si el signo.

.

3.: Si un determinante tiene dos líneas paralelas iguales, vale cero.

.

4.: Si un determinante tiene todos los elementos de una línea iguales a cero, vale cero.

.

5.: Si se multiplican los elementos de una línea por un número, el valor del determinante queda multiplicado por dicho número.

.

6.: Si los elementos de dos líneas paralelas son proporcionales, el determinante vale cero.

.

7..La suma de los elementos de una línea, por los adjuntos de una línea paralela es igual a cero.

.

8.: Si todos los elementos de una línea de un determinante, están formados por la suma de dos sumando, dicho determinante se descompone en la suma de dos determinantes, que tienen los mismos elementos que el determinante dado, excepto los correspondientes a aquella línea, que esta formada por los primeros sumando en el primer determinante y por los segundos sumando, en el segundo.

.

9.: Si los elementos de una línea, son combinación lineal de los de las otras líneas, el valor del determinante es cero.

.

10.: Si a los elementos de una línea se les suma los elementos de otra paralela multiplicados previamente por un número, el determinante no varia.

.

11.: | A.B | = |A|.|B|

.

12.: El determinante de una matriz triangular es igual al producto de los elementos de su diagonal principal.

REGLA DE CHIO.

Si no existe ningún elemento igual a la unidad en el determinante, buscaremos la forma de que al restar dos líneas o que al restar a una línea otra multiplicada por un número obtengamos un uno.

A partir de ese uno y por las propiedades de los determinantes, vamos obteniendo ceros en el determinante, logrando al final que todos los elementos de una línea sean cero excepto el elemento que es igual a uno.

Desarrollando el determinante por los adjuntos de esa línea, obtenemos un determinante de orden una unidad menos que del que partimos.

Haciendo las operaciones anteriores, las veces que sean necesarias, llegaremos a un determinante de tercer o incluso de segundo orden, que resolveremos como ya sabemos.

MATRICES ASOCIADAS A UNA MATRIZ CUADRADA, MATRIZ INVERSA.

Se llama MATRIZ REGULAR, a toda matriz cuadrada cuyo determinante es distinto de cero.

A las matrices cuadradas de determinantes nulos se les llama MATRICES SINGULARES.

Se llama MATRIZ ADJUNTA de una matriz cuadrada A, a la matriz cuyos elementos son los adjuntos de los elementos de la matriz A. A la matriz adjunta de A, se le llama A^d.

Se llama MATRIZ INVERSA de una matriz regular A, a otra matriz B, del mismo orden tal que A.B=B.A=I(M.unidad)

La matriz inversa de A se representa por A^-1 y coincide con la matriz traspuesta de la adjunta de A, dividida por el valor del determinante.

A^-1 = (A^d)^t / |A|

RANGO DE UNA MATRIZ.

Sea A una matriz rectangular de dimensión nxm. Se llama menor de orden h, al determinante de una matriz cuadrada cualquiera de orden h, que está formado por los elementos que pertenecen a h filas y h columnas. Estos menores se obtienen suprimiendo de todas las formas posibles n-h filas y m-h columnas.

Se llama RANGO DE UNA MATRIZ A, al orden h de un menor no nulo, siempre que todos los menores de orden superior a h sean nulos.

El rango de una matriz formada por las componentes de un conjunto de vectores, nos da el número de vectores de ese conjunto que son linealmente independientes.

MÉTODO DE ORLAR, PARA EL CÁLCULO DE RANGOS.

Si a partir de un menor de orden n distinto de cero,

todos los menores de orden n+1 que se pueden formar con los elementos del anterior menor, orlando los elementos de la matriz son cero el rango es n.

PROPIEDADES DEL RANGO DE UNA MATRIZ.

• El rango es único

• Si una línea tiene nulos todos sus elementos, se puede suprimir para calcular el rango.

• Si una linea es proporcional a otra, se puede suprimir para calcular el rango.

• si una linea es combinación lineal de otras, se puede suprimir para calcular el rango.

PERMUTACIONES U ORDENACIONES.

Llamamos permutaciones u ordenaciones de n, a los distintos grupos que se pueden formar con los n elementos, entrando en cada grupo los n elementos, distinguiendose un grupo de otro por el orden de los elementos.

Pn=n!=n(n-1)(n-2)....1

PERMUTACIÓN PRINCIPAL.

Si no se designa previamente llamaremos permutación principal, a la que tiene sus elementos en el orden natural.

PERMANENCIA E INVERSIÓN.

Decimos que dos elementos en una permutación están en permanencia cuando prescindiendo de los demas están en el mismo orden que en la permutación principal. En caso contrario están en inversión.

El número de inversiones se designa a.

CLASE PAR O IMPAR.

Si una permutación presenta en total un número par de inversiones decimos que es de clase par.

TRASPOSICIÓN DE LOS ELEMENTOS DE UNA PERMUTACIÓN.

Si en una permutación se trasponen dos elementos de la permutación, la permutación cambia de clase. (De par a impar o viceversa)